머신러닝 기반 이상 탐지(Anomaly Detection) 기법의 종류

 

이상 탐지(Anomaly Detection)란, 데이터에서 예상과는 다른 패턴을 보이는 개체 또는 자료를 찾는 것을 말한다.
즉 학습 데이터를 기반으로 기존 데이터들과는 다른 특성을 갖는 데이터를 찾는 모형을 만드는 방법이다.
사이버 보안, 의학 분야, 금융 분야, 행동 패턴 분야 등 다양한 분야에 적용될 수 있다.
대표적인 예로 신용카드 사기, 사이버 침입, 테러 행위 같은 악의적 행동이나 시스템 고장, 비정상적인 상황 등에 활용된다.

'이상'이라는 표현은 적용되는 도메인 컨텍스트나 데이터의 종류에 따라 anomaly, outlier, discordant observation, exception, aberration, surprise, peculiarity, contaminant 등 다양하게 불린다.

https://github.com/DHI/tsod 

 

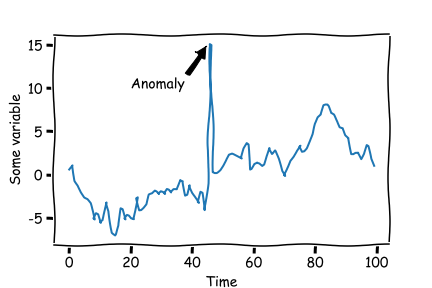
이상 탐지는 종종 분류(Classification) 문제와 혼동되는데, 둘은 엄연한 차이가 있다.
분류는 두 범주를 구분할 수 있는 경계면을 찾는 것인 반면,
이상 탐지는 다수의 범주를 고려해 이상치가 아닌 데이터들의 sector를 구분 짓는 것이라고 할 수 있다.

Noise Detection은 이상 탐지와는 다르다.
노이즈는 분석 이전 단계에서 불필요한 개체 또는 제거해야 할 성분을 말하며, 이를 조정함으로써 통계 모형 추정에서 이상치의 영향을 줄일 수 있다.

또한 Novelty Detection은 지금까지 발견되지 않았던 새로운 패턴을 찾아내는 것을 목표로 한다. 이상 탐지와 달리 novelty는 정상치에 포함된다.

이상 탐지를 위해서는 다양한 접근이 가능하다.
그 기법들을 살펴보면 크게 분류 기반, NN 기반, 군집화 기반, 통계적 기법, 스펙트럴 기법 등으로 나뉜다.

먼저 분류 기반 기법은 분류기를 주어진 특성 공간(Feature space)에서 학습시킬 수 있는 가정을 전제로 한다.
라벨의 개수에 따라 one-class 또는 multi-class로 데이터를 학습시키고, class에 해당하지 않는 개체를 이상치로 처리한다.

분류 기반 기법의 장점은 여러 강력한 분류 알고리즘을 이용할 수 있다는 데 있다.
대표적으로 오토인코더(Autoencoder), 베이지안 네트워크(Bayesian network), 서포트 벡터 머신(SVM, Support Vector Machine), 결정 규칙(Decision Rule) 기반 알고리즘이 있다.

이 중 오토인코더 기반 알고리즘을 조금 더 살펴보자.
신경망의 구조는 아래 그림과 같다.
입력층(Input layer)과 출력층(Output layer)의 노드 수가 같고, 하나 이상의 은닉층(Hidden layer)으로 구성된 인코더를 통해 입력 데이터를 압축하고, 디코더를 사용해 개체를 복원한다.
이렇게 복원했을 때 발생하는 복원 오차가 크면 클수록 이상 개체라고 판단하는 방식이다.
One-class, multi-class 문제의 구분 없이 모두 적용할 수 있다.

두 번째는 NN(Nearest Neighbor) 기반 기법들이다.
이는 정상치가 어떤 근방(Neighbor)에 밀집되어 있고, 이상치가 각 근방에서 멀리 떨어져 있다는 가정을 전제로 한다.
따라서 이 기법을 쓰기 위해서는 두 개체 사이 거리 개념이 정의되어야 하며, 이는 데이터 유형에 따라 여러 방법을 적용할 수 있다. 연속형 변수에 대해서는 일반적으로 유클리드 거리를, 범주형 변수에 대해서는 단순 일치 계수가 자주 쓰인다. 또 다변량 데이터라면 각 변수에 대한 거리를 결합하여 사용할 수도 있다.

이 기법은 대체로 비지도 학습 또는 준지도 학습을 기반으로 하고, 거리 개념만 잘 정의된다면 자료 형태에 구애 받지 않는 장점이 있지만, 테스트 과정에서 각각의 근방을 구해야 하므로 시간이 오래 걸린다.

이와 같은 이상 점수를 구하는 방법은 크게 두 가지로 나뉘는데, k번째로 가까운 개체와의 거리를 이용하거나, 상대 밀도(Relative Density)를 이용하는 방법이 있다.
k번째로 가까운 개체와의 거리를 이용하는 경우, 이상 점수를 기준으로 정렬시킨 뒤 가장 큰 k개를 이상 개체로 보는 방법이다. 이상 점수는 가까운 k개 개체와의 거리의 합으로 구하거나, 한 개체에서 일정 거리 이내에 있는 개체의 수를 세는 방법 등이 있다.

상대 밀도를 이용하는 경우, 각 객체 근방의 밀도를 추정해, 낮은 밀도의 개체를 이상 개체로 판단하는 방법이다.

세 번째는 군집화(Clustering) 기반 기법들이며, 이는 근본 가정에 따라 세 종류로 나뉜다.
첫 번째는 정상치가 하나 또는 몇 개의 군집에 모여 있고, 이상치는 군집에 속하지 않는다는 가정을 바탕으로 한다. 따라서 모든 개체를 군집에 넣지 않아도 되는 DBSCAN, SNN 군집화 등의 알고리즘을 활용한다.
다만 군집을 찾아내는 것이 주된 목적이므로 이상 탐지에 최적화되어 있지 않다는 단점이 있다.

두 번째 그룹은 군집의 중심(Centroid) 중 가장 가까운 것과의 거리가 긴 것을 이상치라고 본다. 먼저 군집화를 하고 개체가 포함된 군집의 중심과 개체 사이 거리를 이상 점수로 놓는 것이다.
학습 데이터를 군집화하고 테스트 개체를 군집과 비교해 이상 점수를 얻는 식이므로 준지도 기법이라고 볼 수 있다.
자기 조직화 지도(SOM, Self-organizing Map), k-Means 등을 이용한다.

세 번째 그룹은 정상치는 크거나 조밀한 군집에, 이상치는 작거나 sparse한 군집에 속한다는 가정을 기반으로 한다.
즉 개체가 속한 군집의 크기나 밀도가 이상 여부를 판단하는 기준이 된다.
이들은 한 쌍의 관측치들 간의 거리 계산이 필요하므로, NN 기반 이상 탐지 기법과 유사하다.
다만 주요 차이점은 군집화 기반 이상 탐지 기법이 자신이 속한 클러스터와 관련해 각 관측치를 평가하는 반면, NN 기반 기법은 가까이 존재하는 로컬 이웃에 대해 각 관측치를 분석한다는 점이다.

네 번째로 통계적 기법은 근본적으로 이상치가 가정된 확률 분포에서 생성되지 않았기 때문에, 부분 또는 완전히 동떨어졌다고 여겨지는 관측값이라고 정의한다. 또한 이상치는 확률 분포에서 낮은 영역에서 나타난다는 가정을 전제로 한다.
주어진 자료로 정상 데이터 모형을 적합한 뒤 통계적 추론을 통해 새로운 개체가 그 모형을 따르는지 판단한다.
모수적, 비모수적 기법을 모두 적용할 수 있으며, 모수적 기법은 분포의 꼴을 미리 알고 있다고 가정하고 모수를 추정하는 반면, 비모수적 기법은 일반적으로 분포에 대한 가정이 없다.
계산 복잡도는 사용하고자 하는 모형의 종류에 따라 달라지는데, 정규, 포아송, 다항처럼 간단한 분포를 쓰면 보통 자료 크기에 선형으로 나타난다. 그러나 혼항 모형이나 은닉 마르코프 모형(Hidden Markov Model) 같은 복잡한 모형은 추정에 반복적인 계산을 요구해 수렴 속도와 기준에 따라 오랜 시간이 걸릴 수 있다. 또한 커널 기반 기법은 자료 크기에 따라 잠재적으로 제곱 시간 알고리즘이다.

 

스펙트럴 기반 기법도 최근 다양하게 적용되고 있다. 이는 변수들의 조합으로 자료의 변동(Variability)을 대부분 설명하도록 자료를 근사한다.
데이터를 더 낮은 차원의 부분 공간(Subspace)으로 보내면(Embed), 그 공간에서는 정상과 이상이 확연히 구분된다는 가정을 전제로 한다.

주로 사용하는 기법이 주성분 분석(PCA, Principal Component Analysis)이다.
데이터를 저차원 공간으로 사영시켰을 때, 데이터의 상관 구조(Correlation Structure)를 만족하는 정상 개체는 사영값이 낮고, 상관 구조에서 벗어난 이상 개체는 높은 값을 보이게 되는 방식이다.

계산 복잡도는 일반적으로 데이터 크기에 선형 시간으로, 차원에는 제곱 시간으로 비례한다.
비선형 기법을 쓰면 차원에 선형이 되도록 줄일 수 있지만, 대신 주성분 개수에 대해 다항식 시간이 된다. 특이값 분해를 사용하는 기법은 자료 크기에 제곱 시간이다.
고차원 데이터 처리에 적합하며, 다른 기법 적용을 위한 전처리처럼 사용하는 것도 가능하다.
그러나 자료를 보낼 저차원 공간에서 정상, 이상치가 제대로 분리되어야만 유용하다.

이 외에도 정보 이론 기반, 맥락적 이상 탐지, 딥러닝 기반의 매우 다양한 기법들이 있다.
모든 기법과 알고리즘을 적용해보고 탐색하는 것은 현실적으로 불가능하므로, 문제와 데이터 형태에 따라 적합한 기법을 고민하는 것이 필요하다.

 

『기계학습(Machine Learning) 기반 이상 탐지(Anomaly Detection) 기법 연구』 연구보고서 2018-16을 정리한 글입니다.