데이터 특성(Feature) 사이 차원의 영향을 제거하고, 서로 다른 지표들을 비교함으로써 패턴을 정확히 파악하기 위해 정규화를 수행합니다.
그렇다면 정규화는 데이터 전처리 과정에서 항상 거쳐야 하는 필수 단계일까요? 언제 정규화가 필요한 걸까요?
이번 글에서는 피처 정규화가 반드시 필요한 세 가지 경우에 대해 정리해 보았습니다.
※ 개인적으로 공부한 내용을 정리한 글입니다. 틀리거나 다른 의견이 있으시면 그냥 지나치지 마시고, 꼭 댓글 남겨 주세요! :)
Why & How
우선 정규화의 목적과 대표적인 방법에 대해 간단히 짚어 보겠습니다.
앞서 언급했듯 정규화는 차원의 영향을 제거하고, 특정 피처에 편향되지 않도록 값의 범위를 일정한 범위 내로 통일시킵니다. 이를 통해 보다 정확한 데이터 패턴을 파악할 수 있어요.
대표적인 방법으로는 선형 함수 정규화 Min-max Scaling와 표준 정규화 Z-score Normalization가 있습니다.
최소-최대 스케일링의 경우 데이터를 선형 변환(Linear Transformation)함으로써 결과 값을 0과 1 사이에 투영되도록 합니다. 즉 데이터를 동일한 비율로 축소하거나 확대하는 방법이며, 수식으로 나타내면 다음과 같습니다.
$$X_{norm} = \frac{X - X_{min}}{X_{max} - X_{min}}$$
표준 정규화는 평균이 0, 표준편차가 1인 정규 분포로 데이터를 투영하는 방법입니다. 기존 데이터 피처의 평균값이 `\mu`, 표준편차가 `\sigma`라고 할 때, 그 수식은 다음과 같습니다.
$$z = \frac{x - \mu}{\sigma}$$
① 수치형 데이터 + `\alpha`
정규화가 반드시 필요한 첫 번째 경우는 수치형 데이터인 경우입니다.
예를 들어 한 사람의 키와 몸무게가 건강에 미치는 영향에 대해 분석한다고 해볼게요. 이때 키는 일반적으로 1.5 ~ 1.8m 범위에, 체중은 40 ~ 100kg 범위에 있습니다.
그러나 이 데이터를 그대로 분석하면 상대적으로 값의 크기가 큰, '체중'이라는 특성에 편향되어 모델이 학습됩니다. 따라서 정확한 결과를 위해서는 정규화가 반드시 필요합니다.
그렇다면 반대로 범주형 데이터의 경우에는 정규화를 하지 않아도 될까요?
범주형 데이터(Categorical Variable)를 모델에 적용하기 위해서는 인코딩(Encoding)을 통해 수치형 데이터로 변환하는 과정이 필요합니다.
가장 일반적인 방법 중 하나인 원핫 인코딩(One-hot Encoding)은 모든 값을 0 또는 1로 변환합니다.
때문에 이미 값이 일정 범위 [0, 1] 내로 변환되었다고 볼 수 있고, 추가로 정규화가 필요하지 않을 수 있어요.
그러나 인코딩을 거쳤음에도 불구하고 정규화를 고려해야 하는 경우들도 있습니다.
우선 원핫 인코딩이 아닌 다른 기법을 적용하는 경우예요. 예를 들어, 범주의 종류가 많은 데이터에 라벨 인코딩(Label Encoding)을 적용한다면 범주의 개수만큼 또다시 값의 범위가 커질 수 있습니다.
또는 개별 범주의 데이터가 많은 경우에 빈도 인코딩(Frequency Encoding)을 적용하면, 역시나 그 빈도만큼 값의 스케일이 커지게 됩니다.
또 다른 경우는 모델의 특성에 따라 모든 피처의 스케일이 같은 범위에 있어야 유리한 경우입니다. 이 내용은 다음과 연결지어 설명할 수 있습니다.
② 비지도 학습 + `\alpha`
데이터의 패턴이 결과에 직접적으로 영향을 미치는 비지도 학습의 경우 반드시 정규화가 선행되어야 합니다.
대표적으로 클러스터링(군집화, Clustering)과 차원 축소(Dimensionality Reduction) 모델을 한 가지씩 예로 들어 볼게요.
k-Means 클러스터링은 k개의 중심점(Centroid)을 기준으로 공간을 나눈 후, 각각에 속한 점들의 평균적인 위치로 중심점을 이동시키는 방식으로 학습합니다. 즉 점들 사이 거리와 그 평균에 따라 결과를 도출하므로, 정규화를 통해 점들이 서로의 상대적인 거리는 유지하면서 일정한 범위 내에 있도록 변환해야 합니다.
PCA(Principle Components Analysis)는 전체 데이터를 잘 표현할 수 있는 주요한 방향(주성분)을 찾는 알고리즘입니다. 이때 가장 분산이 큰 주성분들을 찾아 저차원으로도 원본 데이터를 잘 표현하도록 축소합니다.
그런데 데이터의 스케일이 서로 다를 경우, 스케일이 큰 속성이 주성분이 될 확률이 높아지며 전체 분산도 달라집니다. 따라서 역시나 정규화를 통해 미리 스케일을 통일해야 정확한 주성분을 도출할 수 있습니다.
특히 ①의 경우에서 언급한 것처럼, 범주형 변수를 이미 인코딩했다고 해도 다른 수치형 데이터와 함께 비지도 학습에 적용하는 거라면 추가로 정규화가 필요할 수 있습니다. 이미 0과 1로 이루어진 이진형(Binary) 데이터라도 다른 수치형 데이터와 스케일을 맞춰야 하기 때문입니다.
(사실 이진형 데이터의 경우에는 k-Means나 PCA보다는 각각 목적에 맞는 다른 알고리즘을 적용하는 것이 더 결과가 좋다고 하네요.)
③ 모수적 모델 + `\alpha`
그렇다면 지도 학습의 경우는 어떨까요? 정규화를 하지 않아도 될까요?
예상했겠지만 꼭 그렇지 않습니다. (제목마다 `+ \alpha`가 붙는 이유..)
사실은 조금 더 큰 차원에서 정규화가 권장되는 경우가 있는데, 바로 모수적 모델(Parametric Model)을 이용하는 경우입니다.
대부분의 머신러닝(딥러닝 포함) 모델은 모수적 혹은 비모수적 모델(Non-parametric Model)로 구분됩니다.
모수적 모델이란 가우시안, 베르누이, 푸아송, 지수, 로그 등의 확률 분포를 기반으로 해당 파라미터를 추정하는 모델을 말합니다. 즉 데이터가 특정 확률 분포를 따른다고 가정하며, 모델이 학습을 통해 각 파라미터를 결정하는 방법입니다.
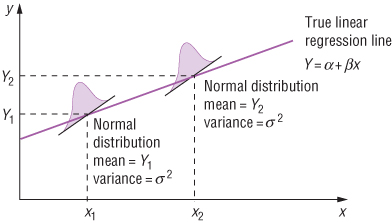
대표적으로 선형 회귀의 경우 가우시안 확률 분포를 따른다고 가정하며, 그에 따라 2개의 고정된 파라미터인 평균과 분산에 따라 정확한 확률 분포의 모양을 결정하게 됩니다.
또한 다음과 같은 간단한 선형 회귀식에서도 계수(Coefficient)에 해당하는 `w`와 절편(Intercept) 또는 편향(Bias)에 해당하는 `b`라는 2개의 파라미터를 찾아볼 수 있습니다.
$$y = wx + b$$
반면 비모수적 모델은 데이터가 따르는 확률 분포에 대한 가정이 없고, 때문에 학습해야 할 파라미터가 정해져 있지 않습니다.
예를 들어 kNN(k Nearest Neighbor)의 경우, 예측하고자 하는 관측치와 가까운 k개의 관측치들의 특성을 이용해 관심 관측치를 예측합니다. 즉 파라미터가 없고, 대신에 2개의 하이퍼파라미터인 k와 거리 측정 방법(유클리디안, 맨해튼 거리 등)이 있습니다.
또는 파라미터와 하이퍼파라미터가 모두 공존하는 경우도 있습니다.
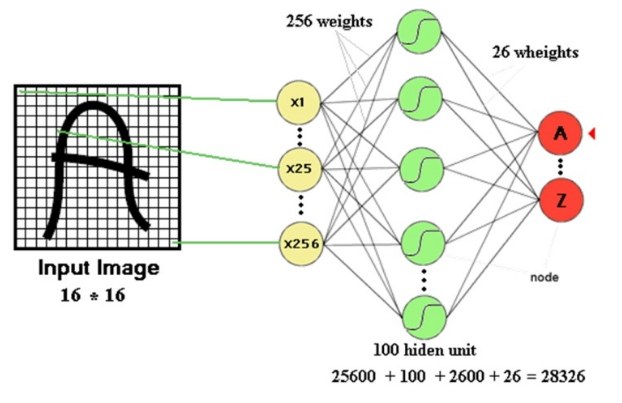
대표적으로 인공신경망(ANN, Artificial Neural Network)이 그렇습니다. 하이퍼파라미터인 노드와 은닉층의 개수를 설정하면, 그에 따라 은닉층(Hidden Layer) 사이를 연결하는 간선의 개수만큼 파라미터를 계산합니다.
이는 파라미터가 존재하기 때문에 넓은 의미에서 모수적 모델로 분류되기도 하지만, 파라미터 계산 시에 확률 분포 개념이 사용되지 않으므로 기본적으로는 모수적 모델과 차이가 있습니다.
따라서 이러한 모델을 세미 모수적 모델(Semi-parametric Model)이라고도 합니다.
그렇다면 이들은 정규화와 어떤 관계가 있을까요?
정확히 말하면 넓은 의미에서의 모수적 모델, 즉 파라미터가 존재하는 모델의 경우 정규화가 필요합니다.
장황하게 설명했지만 사실 그 이유는 간단합니다(수식은 결코 간단하지 않음). 모델의 학습 목표가 바로 파라미터 결정에 있고, 정규화를 통해 그 결정하는 과정(= 최적화)을 효율적으로 만들 수 있기 때문입니다.
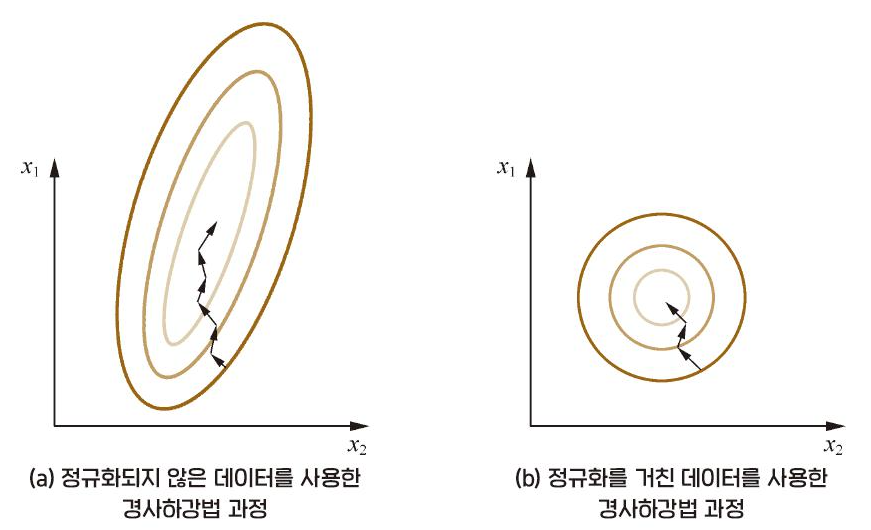
다음은 데이터 정규화가 경사하강법(Gradient Descent) 수렴 속도에 미치는 영향을 나타내는 그림입니다.
학습률이 동일하다는 가정 하에서 그림 (a) `x_1`의 갱신 속도는 `x_2`보다 빠릅니다.
반면 (b)처럼 `x_1`과 `x_2`가 정규화를 거쳐 동일한 수치 구간 내에 있다면, 최적화 목표의 등치선도는 원형으로 변합니다. 때문에 두 피처의 갱신 속도는 동일해지고, 더 빠르게 경사하강법을 이용해 최적 해를 찾을 수 있게 됩니다.
이 내용을 보다 깊게, 수식과 함께 이해하고 싶은 분들은 이 글을 참고하시면 좋을 것 같습니다.
아래 내용을 일부 참고하였습니다.
- 책 『데이터 과학자와 데이터 엔지니어를 위한 인터뷰 문답집』
- Stack Exchange Discussion
- 모수 모델 vs. 비모수 모델
- Stack Overflow Discussion
- Basic Optimization
'공부하며 성장하기 > 인공지능 AI' 카테고리의 다른 글
| [한 줄 정리] 분류 모델 평가 지표 (0) | 2022.01.23 |
|---|---|
| [한 줄 정리] SMOTE (0) | 2022.01.17 |
| 머신러닝 기반 이상 탐지(Anomaly Detection) 기법의 종류 (0) | 2021.11.09 |
| 국소 회귀(Locally Weighted Regression)란? (0) | 2021.08.29 |
| 선형 회귀(Linear Regression)와 경사하강법(Gradient Descent) (0) | 2021.08.23 |