딥러닝을 처음 공부할 때 CNN(Convolutional Neural Network, 합성곱 신경망)에 대해 배웁니다.
일반 신경망 Neural Net과 유사하지만 이미지 데이터의 특성을 인코딩할 수 있고, 또 그 과정에서 네트워크를 학습시키는데 필요한 가중치, 즉 parameter의 수를 크게 줄일 수 있다는 장점이 있습니다.

그런데 CNN은 어떻게 해서 parameter 수를 줄이는 걸까요?
Conv layer(합성곱 층)과 Pooling layer에서 파라미터가 줄어든다는 것은 쉽게 예상해볼 수 있지만, 그 과정을 정확히 설명하기 위해서는 바로 parameter sharing의 개념을 이해해야 합니다.
때문에 이번 글에서는 CNN의 parameter sharing 또는 weights replication에 대해 정리해 보았습니다.
다른 좋은 자료들이 많으니 CNN의 구조와 각 레이어에 대한 설명은 생략하였습니다.
파라미터 수는 정말 줄어들까?
아래 그림은 ImageNet Classification Challenge 2012에 등장한 CNN architecture입니다.
참고로 많이들 아시겠지만 입력 이미지(input)의 크기는 224*224*3이 아니고 227*227*3이 맞습니다. 224는 단순 오타였다고 하네요.

이제 위 실제 예시를 가지고 첫 번째 conv layer의 파라미터 수를 직접 계산해보겠습니다.
일반 뉴럴 넷에서의 가중치를 떠올려 보면, conv layer의 파라미터 수 역시 각 filter의 element 수와 output 뉴런의 개수를 곱한 만큼 생긴다고 예상할 수 있겠네요.
먼저 각 filter의 element 수는 `11 \times 11 \times 3 = 363`개입니다.
그리고 각 filter를 거쳐 생성되는 output 사이즈는 `(227-11)/4 + 1 = 55`, 즉 55*55*96입니다. 이때 96은 CNN의 하이퍼파라미터 중 하나로, filter(또는 feature map)의 개수를 의미합니다.
따라서 output 뉴런의 개수는 `55\times55\times96 = 290,400`개이고, 앞서 구한 filter element 개수에 편향 bias까지 고려하여 곱한 총 파라미터 수는 `(363 + 1) \times 290,400 = 105,705,600`개가 됩니다.
고작 첫 번째 층의 파라미터 수를 구한 것뿐인데, 이미 어마어마하게 많네요.
그 말인즉슨 이게 답이 아니라는 거겠죠!

위 그림은 일반 신경망(왼쪽)과 CNN(오른쪽)의 feed forward를 비교한 것입니다.
일반 신경망은 각 층 사이 모든 노드가 연결되어 있는 반면, CNN은 주변 몇 개 노드만 연결되어 있습니다.
가중치 개수가 줄어들 수밖에 없겠네요!
어떻게 가능할까?
결론부터 말하자면 우리는 앞서 구한 105,705,600개의 파라미터를 34,944개로 대폭 줄일 겁니다.
이것이 가능하려면 한 가지 가정이 필요한데요.
예를 들어 `(x, y)`에서 어떤 patch feature가 유용했다면, 이 feature는 다른 위치 `(x_2, y_2)`에서도 유용할 것이라는 내용입니다.
이를 전제로 각 depth 내의 뉴런들이 같은 가중치와 편향을 가지도록 제한하는 겁니다.
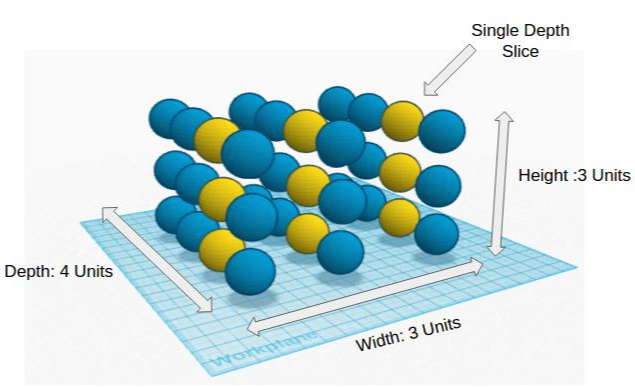
이때 depth는 신경망의 layer 수가 아닌, feature map의 개수를 의미합니다.
즉 depth 방향으로 자른 2차원 slice를 'depth slice'라고 할 때, 각 depth slice 내의 뉴런들이 하나의 파라미터를 서로 '공유'하도록 하는 것입니다.
앞서 했던 계산을 이 parameter sharing 관점에서 다시 해보겠습니다.
filter의 개수가 96개이므로, output에도 96개의 각 depth slice가 존재합니다.
그러나 output 뉴런의 총 개수(`55\times55\times96`)만큼 파라미터가 필요한 것이 아니라, 각 depth slice당 하나의 파라미터만 사용하므로 그냥 96개면 되겠네요.
마지막으로 이를 filter의 각 element 수에 편향을 더한 값과 곱하면, 총 파라미터 수는 `96\times(11\times11\times3 + 1) = 34,944`개가 됩니다.
물론 conv layer 뿐 아니라 pooling layer에서도 아예 spatial한 사이즈를 줄여서 파라미터를 줄이는 기능을 합니다.
하지만 풀링의 경우 직접적인 정보 손실이 있는 반면, 합성곱 연산은 정보 손실 없이 파라미터를 효과적으로 줄일 수 있다는 장점이 있습니다.
아래 자료를 참고했습니다.
'공부하며 성장하기 > 인공지능 AI' 카테고리의 다른 글
| 딥러닝 오차 역전파(Back-propagation) 정확히 이해하기 (0) | 2022.02.15 |
|---|---|
| [한 줄 정리] 베이지안 최적화(Bayesian Optimization) (0) | 2022.02.14 |
| 모델 검증 방법 (0) | 2022.02.07 |
| ROC 곡선 vs. P-R 곡선 (0) | 2022.01.30 |
| [한 줄 정리] 분류 모델 평가 지표 (0) | 2022.01.23 |
