이번 글에서는 뉴럴 네트워크(또는 신경망, Neural Network)에서 가중치(Weights)를 최적화(Optimization) 하기 위해 사용하는 오차 역전파(Back-propagation)의 과정을 직접 계산하면서 이해해보도록 하겠습니다.
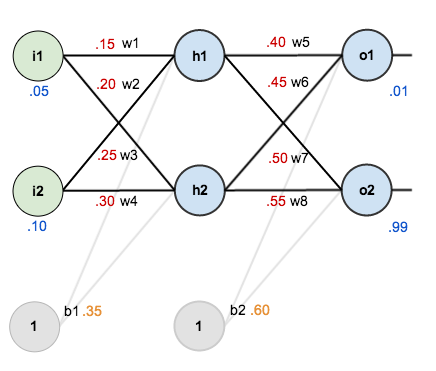
예를 들어 아래 그림과 같은 신경망이 있습니다.
파란색은 input 또는 output 값을, 빨간색은 초기 가중치의 값을 나타냅니다.
① Feed forward
오차역전파를 위해서는 우선 순방향으로 결과 값을 먼저 계산한 후에 그 오차(Error)를 구해야 합니다.
하나씩 순서대로 계산해보겠습니다.
$$net_{h_1} = i_1 * w_1 + i_2 * w_2 + b_1 * 1 = 0.05 * 0.15 + 0.1 * 0.2 + 0.35 * 1 = 0.3775$$
$$out_{h_1} = \frac{1}{1 + e^{-net_{h_1}}} = 0.593269992$$
같은 방법으로 계산하면 `out_{h_2} = 0.596884378`,
따라서 `out_{o_1} = 0.75136507`, `out_{o_2} = 0.772928465`가 됩니다.
② Error 계산
이제 위에서 계산한 결과 값을 이용해서 오차를 계산해보겠습니다.
`E = \sum \frac{1}{2} (target - output)^2`이므로
`E_{total} = E_{o_{1}} + E_{o_2} = \frac{1}{2} (0.01 - 0.75136507)^2 + \frac{1}{2} (0.99-0.772928465)^2`
`= 0.274811083 + 0.023560026 = 0.298371109`
③ Back-propagation
오차역전파는 신경망의 역방향으로 오차의 기울기(Gradient)를 계산해 가중치를 업데이트하는 과정입니다.
따라서 먼저 신경망의 최종 output으로부터 전체 오차의 그래디언트를 계산해보겠습니다.
③-1 마지막 layer에서 오차 gradient 계산
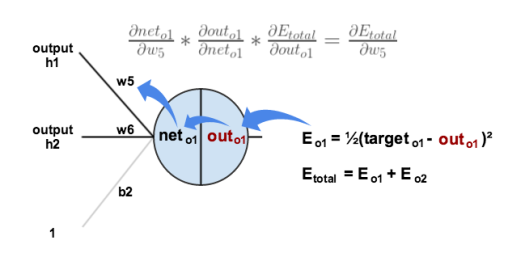
가중치 `w_5`에 대한 전체 오차의 기울기 `\frac{\partial E_{total}}{\partial w_5}`는 Chain rule에 의해 다음과 같이 계산이 가능합니다.
`\frac{\partial E_{total}}{\partial w_5} = \frac{\partial E_{total}}{\partial out_{o_1}} \times \frac{\partial out_{o_1}}{\partial net_{o_1}} \times \frac{\partial net_{o_1}}{\partial w_5}`
위 세 가지 항(term)을 차례대로 구해보겠습니다.
- `\frac{\partial E_{total}}{\partial out_{o_1}} = 2 \times \frac{1}{2} {target_{o_1} - out_{o_1}}^{2-1} \times (-1)`
`= -{target_{o_1} - output_{o_1}} = -(0.01 - 0.75136507) = 0.74136507`
- `out_{o_1} = \frac{1}{1 + e^{-net_{o_1}}}`이므로
`\frac{\partial out_{o_1}}{\partial net_{o_1}} = out_{o_1}(1- out_{o_1}) = 0.75136507 (1-0.75136507) = 0.186815602`
- `net_{o_1} = w_5 * out_{h_1} + w_6 * out_{h_2} + b_2 * 1`이므로
`\frac{\partial net_{o_1}}{\partial w_5} = out_{h_1} = 0.593269992`
따라서,
`\frac{\partial E_{total}}{\partial w_5} = 0.74136507 \times 0.186815602 \times 0.593269992 = 0.082167041`
③-2 해당 가중치 업데이트
이제 위에서 계산한 `w_5`에 대한 오차 `E_{total}`의 편미분, 즉 기울기 값을 이용해 해당 가중치를 업데이트할 수 있습니다. 이를 수식으로 나타내면 다음과 같습니다.
$$w_5^{+} = w_5 - \eta \times \frac{\partial E_{total}}{\partial w_5}$$
이때 `\eta`는 하이퍼파라미터로서 학습률(Learning rate)을 의미하며, 임의로 0.5로 설정해보겠습니다.
따라서 앞서 구한 값들을 이용해 계산해보면, `w_5^{+} = 0.4 - 0.5 \times 0.082167041 = 0.35891648`이 됩니다.
기존 0.4에서 조금 더 작은 값이 되었습니다.
마찬가지로 나머지 가중치도 계산하면, 다음과 같이 업데이트할 수 있습니다.
- `w_6^{+} = 0.45 \to 0.408666186`
- `w_7^{+} = 0.5 \to 0.511301270`
- `w_8^{+} = 0.55 \to 0.561370121`
③-3 은닉층(Hidden Layer)에서 오차 gradient 계산
아직 끝난 게 아닙니다! 바로 은닉층의 가중치 업데이트가 남아있죠.
이를 계산하기 위해서는 역시 은닉층에서 오차의 기울기를 먼저 구해야 합니다. 그 과정은 위 ①에서와 거의 유사하지만, 몇 가지 유념할 부분이 있습니다.
우선, 이번에는 `w_1`에 대한 오차의 기울기를 구해보겠습니다. 역시 Chain rule에 따라 다음과 같이 풀어서 계산이 가능합니다.
`\frac{\partial E_{total}}{\partial w_1} = \frac{\partial E_{total}}{\partial out_{h_1}} \times \frac{\partial out_{h_1}}{\partial net_{h_1}} \times \frac{\partial net_{h_1}}{\partial w_1}`
마찬가지로 세 가지 항을 차례대로 구한 뒤 서로 곱해보겠습니다.
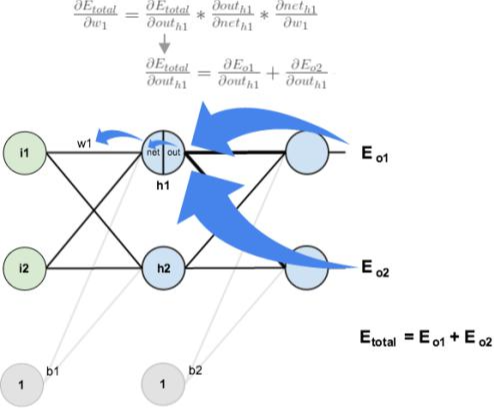
첫 번째 항을 구할 때 주의할 점은 해당 노드에서 오차 `E_{total}`가 여러 노드들의 오차가 더해진 값이라는 사실입니다.
즉, `\frac{\partial E_{total}}{\partial out_{h_1}}`는 `\frac{\partial E_{o_1}}{\partial out_{h_1}}`와 `\frac{\partial E_{o_2}}{\partial out_{h_1}}`를 각각 더해서 계산해야 합니다.
- `\frac{\partial E_{o_1}}{\partial out_{h_1}} = \frac{\partial E_{o_1}}{\partial net_{o_1}} \times \frac{\partial net_{o_1}}{\partial out_{h_1}} = (\frac{\partial E_{o_1}}{\partial out_{o_1}} \times \frac{\partial out_{o_1}}{\partial net_{o_1}}) \times w_5`
`= (0.74136507 \times 0.186815602 ) \times 0.4 = 0.055399425`
이때 또 한 가지 주의할 것은 아직 전체 신경망에 대한 back-prop이 끝나지 않았기 때문에 ②에서 계산한 새로운 `w_5^{+}`가 아닌 기존 `w_5`를 이용해야 한다는 것입니다.
- `\frac{\partial E_{o_2}}{\partial out_{h_1}} = -0.019049119`이므로
`\frac{\partial E_{total}}{\partial out_{h_1}} = 0.055399425 + (-0.019049119) = 0.036350306`
나머지 두 항은 이전에 계산한 값들로 비교적 빠르게 계산이 가능합니다.
- `out_{h_1} = \frac{1}{1+e^{-net_{h_1}}}`이므로
`\frac{\partial out_{h_1}}{\partial net_1} = out_{h_1}(1 - out_{h_1}) = 0.59326999(1-0.59326999) = 0.241300709`
- `net_{h_1} = w_1 * i_1 + w_2 * i_2 + b_1 * 1`이므로 `\frac{\partial net_1}{\partial w_1} = i_1 = 0.05`
따라서,
`\frac{\partial E_{total}}{\partial w_1} = 0.036350306 \times 0.241300709 \times 0.05 = 0.000438568`
③-4 해당 가중치 업데이트
이제 위 계산 결과를 이용해 나머지 가중치들도 업데이트할 수 있게 되었습니다.
각 값을 계산하면 다음과 같습니다.
- `w_1^+ = 0.15 \to 0.149780716`
- `w_2^+ = 0.2 \to 0.19956143`
- `w_3^+ = 0.25 \to 0.24975114`
- `w_4^+ = 0.3 \to 0.29950229`
이렇게 오차 역전파가 마무리되었습니다.
이 과정을 통해 오차에는 어떤 변화가 있었을까요?
처음 순방향으로 계산했을 때 오차는 0.298371109였습니다.
그리고 우리가 새로 업데이트한 가중치들을 적용할 경우, 오차는 0.291027924로 줄어드는 것을 확인할 수 있습니다.
추가로 이러한 과정을 반복한다면 더 크게 오차가 줄어들겠죠!
실제로 10,000번을 반복할 경우, 전체 오차는 무려 0.0000351084로 줄어듭니다.
이때 `out_{o_1}`은 0.015912196으로, target인 0.01과 거의 유사하게 나타납니다.
또한 `out_{o_2}`는 0.984065734로, target인 0.99와 매우 유사함을 확인할 수 있습니다.
아래 자료를 정리하였습니다.
'공부하며 성장하기 > 인공지능 AI' 카테고리의 다른 글
| YOLOv3 모델 학습 속도 개선하기 (0) | 2022.06.18 |
|---|---|
| 서포트 벡터 머신(Support Vector Machine) (0) | 2022.02.21 |
| [한 줄 정리] 베이지안 최적화(Bayesian Optimization) (0) | 2022.02.14 |
| CNN Parameter Sharing (1) | 2022.02.10 |
| 모델 검증 방법 (0) | 2022.02.07 |
