과적합(Overfitting)이란 모델이 train 데이터에 지나치게 적응되어 그 외의 데이터에는 제대로 대응하지 못하는 상태를 말한다.
이게 과연 무슨 말일까? 데이터를 잘 학습할수록 좋은 것 아닌가?
예를 들어 아래와 같은 회귀 문제가 있을 때, 우리가 원하는 모델은 두 번째에 가깝다.
첫 번째 모델은 과소적합(Underfitting)의 경우로, 주어진 데이터를 아직 제대로 반영하지 못하고 있고,
세 번째 모델은 주어진 데이터가 모든 경우에 나타나는 일반적인 경향이라고 오해한 경우이다.
즉 과적합(Overfitting)되어 새로운 데이터에 대해서는 적용할 수 없는, 일반화하기 어려운 경우이다.
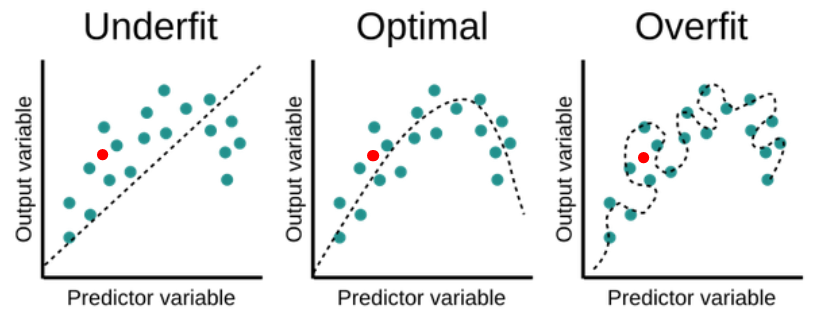
세 그래프에 빨간 점(data)을 하나씩 더 찍어 보았다.
점선(모델이 예측한 결과)과의 거리가 가장 가까운 모델은 무엇인가?
모든 input 데이터에 대한 오차가 존재하지만, 그럼에도 대체적으로 가장 데이터의 분포와 경향을 잘 나타내고 있는 것은 바로 두 번째 모델이다.
오버피팅된 세 번째 모델의 경우 기존 데이터들은 오차 없이 모두 표현해냈지만, 새로운 데이터가 주어지자 오히려 예측한 값의 오차가 더 크게 나타났다.
이처럼 좋은 모델, 즉 모델의 성능이 좋다는 것은 얼마나 범용적 인가와 직접적으로 연결된다.
모델의 성능은 곧 일반화 성능을 말한다고도 볼 수 있다.
따라서 주어진 데이터를 잘 학습해서, 그것을 잘 표현해내는 모델을 만드는 것이 우리의 목표이지만,
동시에 과적합을 방지함으로써 지나치게 train 데이터에 의존적이지 않도록 해야 한다.
과적합이 일어나는 이유
과적합이 일어나는 이유는 다양하지만, 주로 아래 두 가지의 경우에 발생한다.
- feature(→ parameter)가 많고 표현력이 높은 모델인 경우 (상대적으로 데이터 수가 적은 데 비해)
- train 데이터가 적은 경우 (상대적으로 feature → parameter 가 많은 데 비해)
위 두 가지 조건을 충족시켜서 실제 코드로 오버피팅을 재현해보자.
일부러 MNIST 데이터셋에서 6만 개 중 300개만을 train 데이터로 사용하고, layer가 7층이면서 각 층의 노드는 100개인 매우 복잡한 네트워크를 만든다.
(전체 소스코드는 여기에서 확인 가능)
# 데이터셋 로드
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# overfitting 재현을 위해 데이터 300개만 사용
x_train = x_train[:300]
t_train = t_train[:300]
# input_size: mnist dataset의 dimension = 784
# 각 layer의 노드 수 = 100개
# hidden_size_list: hidden layer가 6개이면 network layer가 7개
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=100)
optimizer = SGD(lr=0.01)
max_epochs = 201
train_size = x_train.shape[0]
batch_size = 100
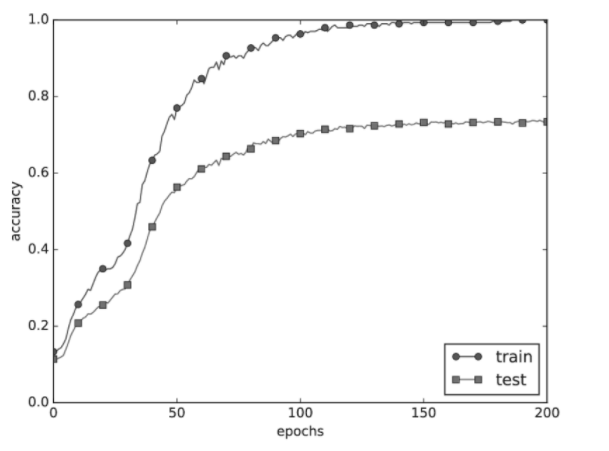
이렇게 해서 학습시킨 각 epoch에 따른 accuracy를 그래프로 그려보면 다음과 같다.
train accuracy는 epoch이 증가함에 따라 거의 1.0에 수렴하면서 매우 높아지는 데 비해,
test accuracy는 점점 train accuracy와의 차이가 벌어지면서 약 0.7 수준에 머물고 있다.
이처럼 train에 비해 test 성능이 낮고 그 차이가 크다면 과적합이 발생한 것이라고 판단할 수 있다.
과적합을 방지하는 방법
안타깝게도 과적합을 완벽히 피할 수는 없다. 다만 어떻게 완화하고, 그에 따른 성능 저하를 최소화할 것인가에 집중해야 한다.
그렇다면 과적합을 가능한 한 억제할 수 있는 방법에는 어떤 것들이 있을까?
쉽게 생각해보면 과적합이 일어나는 조건의 반대 상황을 만들어주면 된다!
즉 1) input 데이터를 늘리거나, 2) parameter를 줄이면 되는데 사실 데이터를 더 수집해서 수를 늘리는 방법은 대부분의 경우 어렵기 때문에 feature를 줄이는 것을 중점적으로 고려할 수 있다.
feature의 개수를 줄이는 방법은 사람이 판단해 manually select 하는 방법과 model이 select하게끔 하는 방법이 있다.
그러나 사실 어떤 feature가 얼마나 유용할지 알 수 없기 때문에 이 또한 적용하기가 쉽지 않다.
대신에 우리가 찾을 수 있는 방법은 각 feature마다 페널티(규제)를 부여해서 그 영향력을 조정하는 것이다.
이러한 방법을 정칙화 또는 규제 Regularization라고 한다.
💡 잠깐!
Regularization이라는 말은 '정규화'라고도 불리며 Normalization과 혼동되는 경우가 많다.
또 이 normalization은 표준화(Standardization)와도 자주 헷갈리는 개념이다.
이들의 개념(차이)을 정리하자면,
- 정규화 Normalization은 데이터의 분포가 정규분포에 가깝게 만드는 것, 즉 범위(scale)를 0~1 사이 값으로 바꾸는 것
- 표준화 Standardization은 데이터가 표준 정규분포에 가깝게 만드는 것, 즉 평균이 0이고 분산이 1이 되도록 scaling 하는 것
- 정칙화 Regularization은 오버피팅을 방지하기 위해 weight에 penalty를 부여하는 것이라고 할 수 있다.
이 regularization에도 가중치 감소(Weight Decay), 드롭아웃(Dropout), 배치 정규화(Batch Normalization) 등 다양한 방법이 있지만, 이번 글에서는 가중치 감소와 드롭아웃에 대해서만 다뤄보기로 한다.
① 가중치 감소(Weight Decay)
가중치 감소는 모델의 학습 과정에서 가중치에 페널티(규제)를 부여함으로써 과적합을 방지하는 방법이다.
가중치 `W` 가 클수록 더 큰 페널티를 부과해 해당 input `x`에 대해 지나치게 fit하지 않도록 조절하는 것이다.
이때 페널티를 얼마나 부과할 것인지를 계산하는 방법이 L1 또는 L2 Regularization이다.
각각의 계산식은 다음과 같다.
- L1 규제 regularization
$$L_{new} = L_{old} + \lambda \sum \left | W \right |$$
- L2 규제 regularization
$$L_{new} = L_{old} + \frac{\lambda }{2n}\sum W^2$$
위 식에서 `L`은 손실함수(Loss Function)를, `\lambda`는 규제 강도(Regularization Strength), 즉 규제의 정도를 결정하는 하이퍼파라미터를 의미한다.
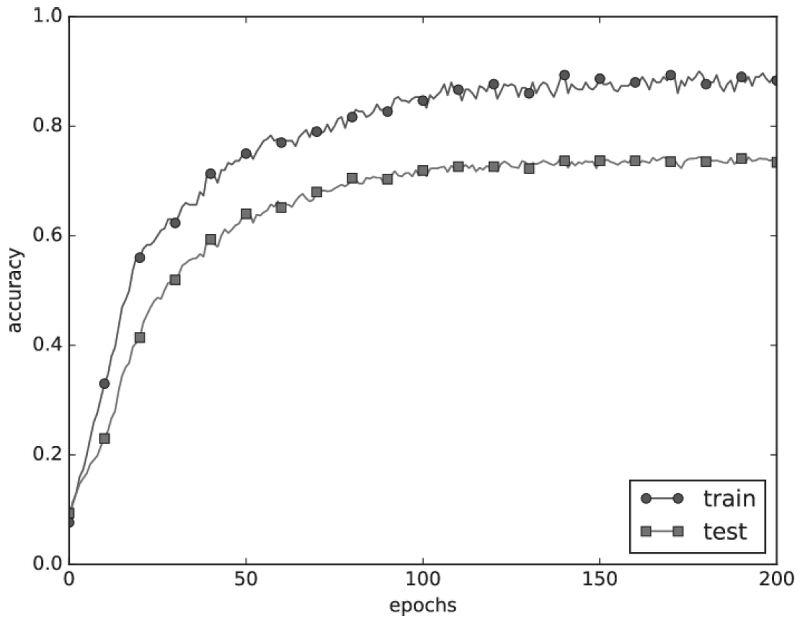
이렇게 규제를 적용하면, 위에서 보았던 epoch에 따른 accuracy 그래프가 아래와 같이 바뀐다.
과적합이 억제되어 train과 test 데이터셋에 대한 차이가 줄어든 것이다.
② 드롭아웃(Dropout)
신경망이 복잡해질수록 위에서 살펴본 규제만으로는 과적합을 방지하기 어렵다.
이럴 때 적용할 수 있는 것이 바로 드롭아웃이다.
드롭아웃은 뉴런을 임의로 삭제하면서 학습하는 방법을 말한다.
train 하면서 무작위로 은닉층(Hidden Layer)의 뉴런을 골라 배제하고, 다음 layer로 신호를 전달하지 못하도록 하는 것이다.

실제 코드에서는 keras 라이브러리를 이용해 매우 간단하게 드롭아웃 layer를 추가할 수 있다.
아래 예시에서는 dropout layer에 0.5라는 값을 주어서 뉴런의 절반만 학습에 이용하도록 하였다.
# keras를 이용해 dropout layer를 적용한 예시
from tensorflow import keras
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation='relu'),
keras.layers.Dropout(0.5),
keras.layers.Dense(10, activation='softmax')])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.fit(x_train, y_train, epochs=10)
이러한 기법은 결과적으로 앙상블 학습을 구현한 것과 유사한 효과를 낸다.
앙상블 학습을 통해 여러 모델의 평균을 내는 것과 비교해 보면, 그 결과는 비슷하지만 훨씬 더 적은 계산 비용이 든다는 장점이 있다.
“It is better to be approximately right than precisely wrong.”
By Warren Buffett
아래 내용을 참고했습니다.
- 책 『밑바닥부터 시작하는 딥러닝』
- Machine Learning Lecture by Andrew Ng
- 7 Simple Techniques to Prevent Overfitting
'공부하며 성장하기 > 인공지능 AI' 카테고리의 다른 글
| [Kaggle] Recruit Restaurant Visitor Forecasting Competition (0) | 2021.08.21 |
|---|---|
| 하이퍼파라미터(Hyperparmeter)와 최적화(Optimization) (0) | 2021.08.18 |
| 앙상블 학습(Ensemble Learning)이란? (2) | 2021.08.15 |
| 경사하강법(Gradient Descent)이란? (0) | 2021.07.27 |
| 수치 미분(Numerical differentiation)이란? (0) | 2021.07.27 |
